fluency

The Secret to Speed Tests Revealed, Part I

can't keep a Secret
Standard

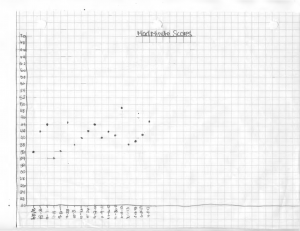
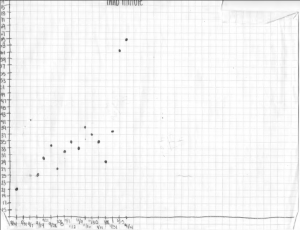
I was never a big fan of speed tests in my early years of teaching, but once I learned how to use them effectively, they became a regular part of teaching. In this 3-part series of posts, I will map out the process I used with speed ‘tests’ to improve math fluency. I used them weekly the last 5 or so years of my teaching, and was very pleased with the results (Scroll down to see results from two of my students).

 

1. They are NOT Speed Tests!

First, let’s start with the nomenclature, “Speed Tests”. I am more concerned with building math fluency, not testing speed in adding or multiplying. Additionally, the word ‘test’ has a negative connotation to many students. So I never called them ‘Speed Tests’; I wanted to make it more catchy and make it fun. So I always called them the common and popular, “Mad Minute”.

2. The Keys to Effectiveness

Speed drills can be used to build fluency, if done correctly. Remember, math fluency is developed over time, through repetition, with immediate feedback; not created in a day with a single speed drill. Doing a speed ‘test’ once a grading period or once a semester– is just that, a test. My goal was to make my kids better math students.

Effective uses of speed drills need to have the “Five Keys to Building Fact Fluency”. The Keys are:

  • Repetition
  • Time Constraints
  • Immediate/Near-Immediate Feedback
  • Allow for Failure
  • Gradual Increases in Difficulty

3. Implementing in Your Classroom

I did Mad Minute (almost) every week on Friday as the opening activity of class, (and once my kids were trained) the whole process took 5-7 minutes. Implementing quickly and efficiently in the classroom requires organization, a well-defined process, and training of your kids. Doing the Mad Minute regularly allowed the students to be prepared to do the drills.  After the activity was finished, my kids were settled, we’ve ‘activated their thinking’ and we were ready to start a lesson or take a quiz.

My Process:

  • Greeted my students (with a smile and interest)
  • Students went to their seats and took out dry-erase markers and the mad minute sheet
  • Set the timer on the smart board
  • Go! Mad Minute!
  • Students self-grade and record results on their charts
  • Students put away the dry-erase markers and mad minute sheet

In the next post I will cover this process in much more detail.

 

4. The Results

The images below are graphs plotting the number of correct digits doing a 2-digit multiplication speed drill over the full school year. Every month or so I increased the difficulty of the speed drill, so these graphs not only show an increase of speed & accuracy, they also show an increase in being able to do more difficult problems.

madminutegraphs2

Click for larger view

Click for a larger view


As you can see from the scatter plots, the trend of the points is increasing, meaning the kids are getting more accurate and faster (ie, more fluent!). I will discuss more about these graphs in part 3 of the series.

 

What are your frustrations about doing (or trying to do) Speed Drills? What has worked for you? What doesn’t work? Leave a comment and share with the community.

The Importance of Being Fluent, Part II

Child sitting test
Standard

At the end of my previous post, I hinted at another reason why fluency is important for students and how they can “go even faster…”.

Fluency is not only the ability to recall effortlessly and accurately, but also the ability to recognize patterns and to apply shortcuts and ‘tricks’ correctly. For example, in teaching data analysis units, some students have problems with finding means– either forgetting to divide, or more usually, making a mistake in the addition of the set of numbers and getting an unending decimal when they try to divide. For example:

Find the mean of the following numbers:
5 + 9 + 4 + 3 + 2 + 8 + 6 + 7 + 1 + 10= ? (this equals 55!)

To a student who is not fluent in addition, this looks hard! The student thinks, “Too many numbers to add up. Then I have to divide. And I’ll probably get a decimal that doesn’t end…” The student has no confidence in themselves, and will not want to apply the effort to add all the numbers.

However, you may have seen it quickly because you are fluent in adding 1-digit numbers:

8 + 2 = 10          7 + 3 = 10             6 + 4 = 10               9 + 1 = 10  

What’s left? 5 and a 10.  Obviously, much easier to add 10 + 10 + 10 + 10 + 10 + 5 = 55.

I understand that this is a specific, made up example to illustrate my point, but the fact the fluency allows us to instantly see ‘groups’ of 10’s makes the addition go much faster and easier.

What about multiplication? Teachers, have you seen this? (I did in 7th grade):

   413
x 200 
    000
  0000
82600

as opposed to this:

413
  x 200
82600

or even this: “I know that I can just add two zeros at the end since I am multiplying by 200. And since 4×2=8, 1×2=2, 3×2=6, the answer is 82,600”

The problem with this multiplication problem is writing down way too much information (then consider how bad some handwriting can be, especially boys!)– which can introduce mistakes – not related to actual multiplication– but to organization. Forgetting to add a place holder 0, or lining up the columns correctly, OR actually multiplying incorrectly. And this example does not have any carry values.

The second example is a lot less writing and computing, so there is a lot less chance for error. The last example there is only single-digit multiplication.

I am all for students to learn ‘tricks’ and shortcuts…ONLY after I know they have mastered basic addition and multiplication. One of the problems that occurs when students learn a trick before mastery and understanding is that they will apply the shortcut incorrectly. Teaching tricks and shortcuts over process can lead to confusion on the student’s part.

So, the importance of being fluent is that it allows students to go faster, make fewer mistakes, and be more accurate. Under the pressure to perform well on standardized tests, I firmly believe students who are fluent have a huge advantage of those who still have to compute 5 + 9 + 4 + 3 + 2 + 8 + 6 + 7 + 1 + 10.